Hi, this is Alex, the developer that works on Repper under the hood. We've been working on something a bit different, and we're excited to share it with you: Repper Labs.
Repper Labs is our new experimental playground. It's a place where we tinker with the new render engine we've been building over the past year. We want to explore ideas that push Repper a bit more beyond traditional pattern making. Think of it as the workshop behind the scenes, where we try out techniques that might (or might not!) find their way into the main app someday.
Right now, Labs hosts the first experiment that we want you to play with: Fractals. It takes an image you provide and transforms it into a different kind of pattern, more complex and more exciting.
This blog post is in a slightly more long-form than our other posts; as a developer I'd like to bring you along for a slightly deeper ride.
Fractals: Image-based Julia and Mandelbrot sets
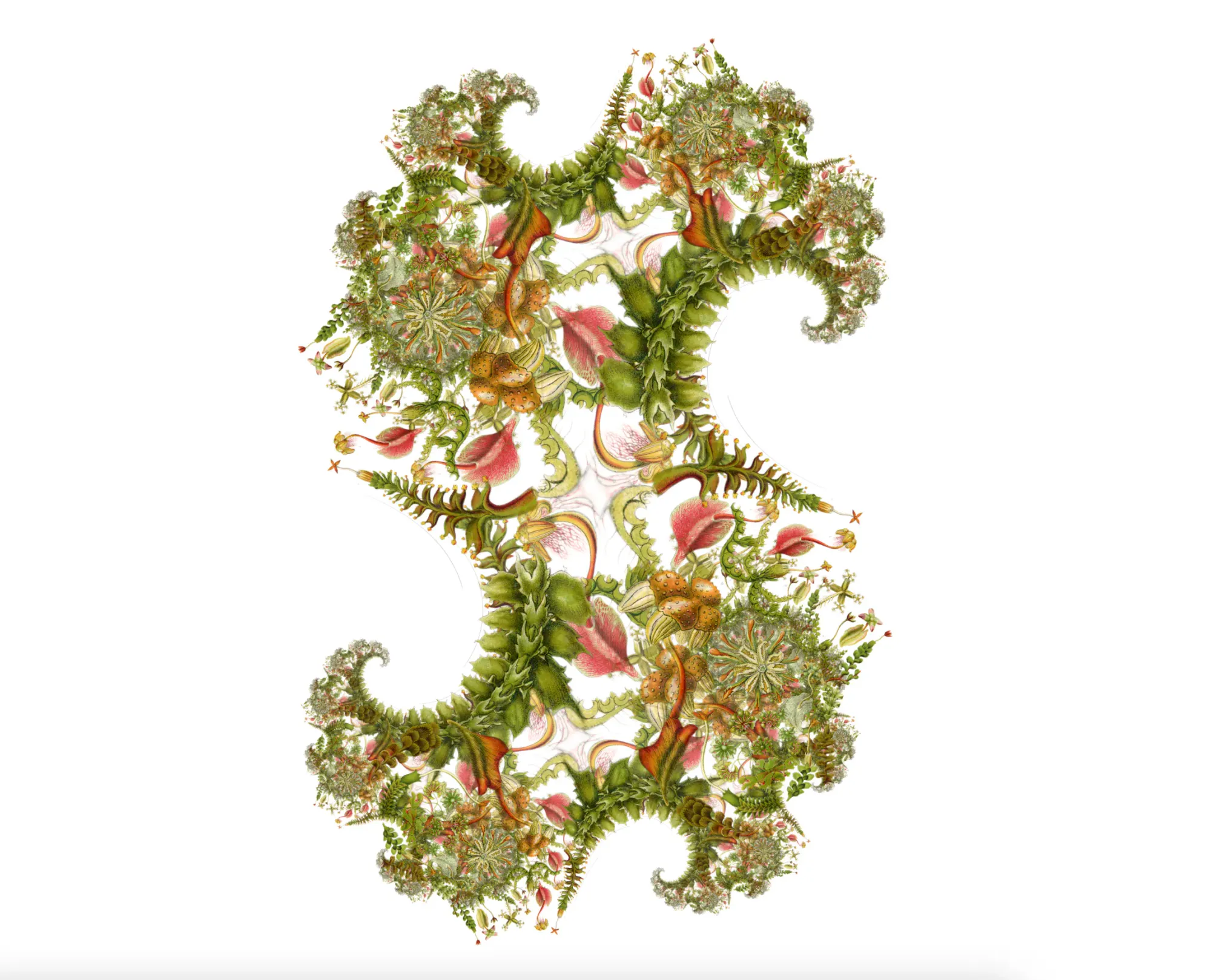




You've probably seen fractal images before—those infinitely detailed swirls and spirals that seem to go on forever as you zoom in. The most famous is the Mandelbrot set, discovered by mathematician Benoît Mandelbrot in the 1970s. Its cousin, the Julia set, is just as mesmerizing and is named after French mathematician Gaston Julia.
Both are generated using a deceptively simple formula: take a complex number, square it, add a constant, and then repeat it many, many times. Whether the calculated point flies of to infinity or stays within bounds determines whether it's "in" the set or not. The beautiful coloured images you've probably seen before typically pick color based on how many steps it takes for a point to shoot off toward infinity (called escape time).

If you want a bit more in-depth information on how the Mandelbrot set is constructed you can watch the excellent video by Numberphile (warning, nerdy talk awaits 😄):
Using images instead of color gradients (aka Orbit traps)
Our fractal experiment uses a different technique called orbit trapping. Instead of counting steps before the point "escapes", we track the path a point takes as we repeatedly run the calculation on it. As it moves, we check how close it gets to a predefined shape, which we call the "trap".
In traditional fractal renderers, the trap might be a point, line, or circle. But here's where it gets interesting: the trap can also be an image. When a point's orbit passes close to the trap region, we sample a color from the image at that position.
The result? Your photograph, illustration, or pattern gets twisted and repeated through the fractal's infinite structure. Flowers become spiraling galaxies. Portraits fragment into kaleidoscopic vortices. It's a bit like putting your image through a mathematical hall of mirrors.
Under the Hood
For those curious about how this actually works, here's a simplified version of the algorithm. For each pixel on screen, we run something like this:
function getPixelColor(pixelPosition, C, trapImage): z = pixelPosition // Start at this pixel's complex coordinate for iteration from 0 to MAX_ITERATIONS: z = z² + C // The core Julia set formula // Check if z is inside our image trap region if z is within trapImage bounds: // Sample color from the image at z's position return trapImage.colorAt(z) // Check if we've escaped (point will go to infinity) if |z| > 2: return backgroundColor // Never escaped, never trapped return backgroundColor
The magic is in that simple z = z² + C line. Each pixel starts at its own position and gets transformed repeatedly. Some orbits quickly shoot off to infinity. Others spiral inward. And some pass through the region where your image sits—that's when we "trap" them and grab a color.
The constant C is what distinguishes different Julia sets. Change it slightly and you get an entirely different fractal structure. In the Mandelbrot set, by contrast, each pixel uses its own position as C and always starts z at zero—which is why the Mandelbrot acts as a kind of "map" of all possible Julia sets.
A note for the technically curious: We render everything on the GPU using WebGL shaders, which is why it's so responsive. Each pixel runs this loop in parallel, making real-time exploration possible. The tradeoff is that we're limited to 32-bit floating-point precision, which puts a ceiling on how far you can zoom in before things get pixelated. (If you've ever explored deep Mandelbrot zooms, you know this is a common constraint!)
What You Can Do
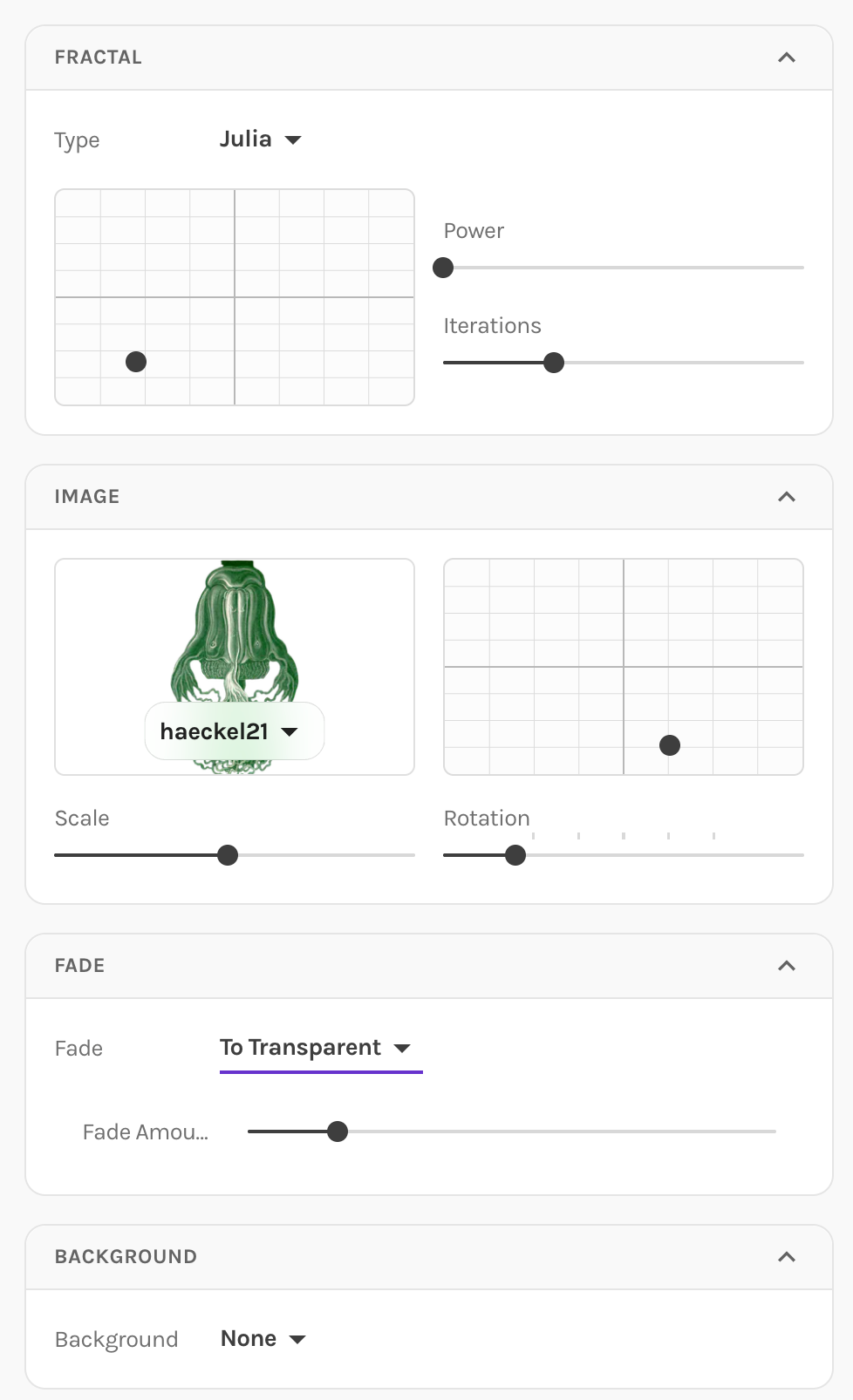
- Choose your fractal: Switch between Julia and Mandelbrot sets.
- Adjust the C value: This parameter (the constant we add each iteration) dramatically changes the fractal's shape. Small changes create entirely different patterns. It's the grid box right under the fractal type.
- Upload any image: JPEG, PNG, or even SVG—we'll use it as the orbit trap. We also provide a number of interesting example images. A number of them are from Ernest Haeckel's Kunstformen der Natur book.
- Transform your source: Translate, rotate, and scale the input image to control where and how it appears.
- Fade: Make higher iterations fade to transparency for a sense of infinite depth.
- Pick your background: Transparent (great for compositing) or a solid color.
- Smooth animations: When you change values, the fractal smoothly morphs to its new state.
Dive deeper
If you want to dive deeper into orbit traps, Inigo Quilez's article on geometric orbit traps is excellent—he pioneered many techniques for using images as traps in real-time rendering. For galleries of fractal art, check out Jock Cooper's extensive collection or the critical writing at Orbit Trap, a blog dedicated to fractal art criticism and curation.
Go Explore
This is just the beginning. Repper Labs is our space for trying things out, and we're curious what you'll make with these tools.
Have questions or feedback? We'd love to hear from you. And if you're not already using our main pattern-making app, give Repper a try—it's free to start.
Happy experimenting!
— Alex & Wouter
Make beautiful geometric patterns with Repper
Instant results · 14 days free access · No strings attached
Create your own pattern
